Homework¶
Homework 1¶
2-1 If the depth of an AVL tree is 6 (the depth of an empty tree is defined to be -1), then the minimum possible number of nodes in this tree is:
-
A. 13
-
B. 17
-
C. 20
-
D. 33
Answer
D. 要么使用 \(n_h = n_{h-1} + n_{h-2} + 1\),要么使用 \(n_h = F_{h+3} - 1\)
2-2 Insert 2, 1, 4, 5, 9, 3, 6, 7 into an initially empty AVL tree. Which one of the following statements is FALSE?
-
A. 4 is the root
-
B. 3 and 7 are siblings
-
C. 2 and 6 are siblings
-
D. 9 is the parent of 7
Answer
B. 3 和 7 不是兄弟节点
graph TD
classDef null fill:#999,stroke:#333,stroke-width:4px
4((4))-->2((2))
4-->6((6))
2-->1((1))
2-->3((3))
6-->5((5))
6-->9((9))
9-->7((7))
9-->a((n)):::null2-3 For the result of accessing the keys 3, 9, 1, 5 in order in the splay tree in the following figure, which one of the following statements is FALSE?
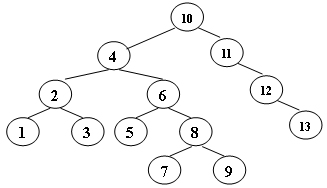
-
A. 5 is the root
-
B. 1 and 9 are siblings
-
C. 6 and 10 are siblings
-
D. 3 is the parent of 4
Answer
D. 4 才是 3 的父节点
graph TD
classDef null fill:#999,stroke:#333,stroke-width:4px
5((5))-->1((1))
5-->9((9))
1-->a((n)):::null
1-->2((2))
2-->b((n)):::null
2-->4((4))
4-->3((3))
4-->c((n)):::null
9-->6((6))
9-->10((10))
6-->d((n)):::null
6-->8((8))
8-->7((7))
8-->e((n)):::null
10-->f((n)):::null
10-->11((11))
11-->g((n)):::null
11-->12((12))
12-->h((n)):::null
12-->13((13))2-4 When doing amortized analysis, which one of the following statements is FALSE?
-
A. Aggregate analysis shows that for all \(n\), a sequence of \(n\) operations takes worst-case time \(T(n)\) in total. Then the amortized cost per operation is therefore \(T(n)/n\)
-
B. For potential method, a good potential function should always assume its maximum at the start of the sequence
-
C. For accounting method, when an operation's amortized cost exceeds its actual cost, we save the difference as credit to pay for later operations whose amortized cost is less than their actual cost
-
D. The difference between aggregate analysis and accounting method is that the later one assumes that the amortized costs of the operations may differ from each other
Answer
B. 势能函数应该在一开始最小
2-5 Consider the following buffer management problem. Initially the buffer size (the number of blocks) is one. Each block can accommodate exactly one item. As soon as a new item arrives, check if there is an available block. If yes, put the item into the block, induced a cost of one. Otherwise, the buffer size is doubled, and then the item is able to put into. Moreover, the old items have to be moved into the new buffer so it costs \(k+1\) to make this insertion, where \(k\) is the number of old items. Clearly, if there are \(N\) items, the worst-case cost for one insertion can be \(\Omega (N)\). To show that the average cost is \(O(1)\), let us turn to the amortized analysis. To simplify the problem, assume that the buffer is full after all the \(N\) items are placed. Which of the following potential functions works?
-
A. The number of items currently in the buffer
-
B. The opposite number of items currently in the buffer
-
C. The number of available blocks currently in the buffer
-
D. The opposite number of available blocks in the buffer
Answer
D. 为了证明,先设 \(\text{size}_i\) 为第 \(i\) 次插入前缓冲区的大小,则易得实际代价 \(c_i\) 在缓冲区未满时等于 \(1\),已满时等于 \(\text{size}_i + 1\),接下来来看各个选项。
A: 若缓冲区未满,则 \(\hat{c}_i = c_i + \phi_i - \phi_{i-1} = 1 + 1 = 2\);若缓冲区已满,则 \(\hat{c}_i = \text{size}_i + 1 + 1 = \text{size}_i + 2\)。无法表现出均摊复杂度为 \(O(1)\),错误。
B: 若缓冲区未满,则 \(\hat{c}_i = 1 - 1 = 0\);若缓冲区已满,则 \(\hat{c}_i = \text{size}_i + 1 - 1 = \text{size}_i\)。无法表现出均摊复杂度为 \(O(1)\),错误。
C: 若缓冲区未满,则 \(\hat{c}_i = 1 - 1 = 0\);若缓冲区已满,则 \(\hat{c}_i = \text{size}_i + 1 + \text{size}_i - 1 = \text{size}_i\)。无法表现出均摊复杂度为 \(O(1)\),错误。
D: 若缓冲区未满,则 \(\hat{c}_i = 1 + 1 = 2\);若缓冲区已满,则 \(\hat{c}_i = \text{size}_i + 1 - \text{size}_i + 1 = 2\)。由此可见均摊复杂度为 \(O(1)\),正确。需要注意的是,这里的势能函数在最开始并不是最小值,但是由于题目强调了最后缓冲区是满的,所以 \(\phi_N - \phi_0 \ge 0\),\(\sum_{i=1}^N \hat{c}_i \ge \sum_{i=1}^N c_i\) 仍能成立。
Homework 2¶
2-1 In the red-black tree that results after successively inserting the keys 41; 38; 31; 12; 19; 8 into an initially empty red-black tree, which one of the following statements is FALSE?
-
A. 38 is the root
-
B. 19 and 41 are siblings, and they are both red
-
C. 12 and 31 are siblings, and they are both black
-
D. 8 is red
Anwser
B. 41 是黑色的
graph TD
classDef null fill:#999,stroke:#333,stroke-width:4px
style 8 fill:#F44336,stroke:#333
style 19 fill:#F44336,stroke:#333
38((38))-->19((19))
38-->41((41))
19-->12((12))
19-->31((31))
12-->8((8))
12-->a((n)):::null2-2 After deleting 15 from the red-black tree given in the figure, which one of the following statements must be FALSE?
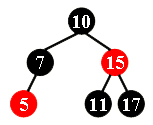
-
A. 11 is the parent of 17, and 11 is black
-
B. 17 is the parent of 11, and 11 is red
-
C. 11 is the parent of 17, and 11 is red
-
D. 17 is the parent of 11, and 17 is black
Answer
C. 若用 11 替换 15,则 11 为黑色,17 为红色;同理可得,若用 17 替换 15,则 17 为黑色,11 为红色。
graph TD
classDef null fill:#999,stroke:#333,stroke-width:4px
style 5 fill:#F44336,stroke:#333
style 17 fill:#F44336,stroke:#333
10((10))-->7((7))
10-->11((11))
7-->5((5))
7-->a((n)):::null
11-->b((n)):::null
11-->17((17))2-3 Insert 3, 1, 4, 5, 9, 2, 6, 8, 7, 0 into an initially empty 2-3 tree (with splitting). Which one of the following statements is FALSE?
-
A. 7 and 8 are in the same node
-
B. the parent of the node containing 5 has 3 children
-
C. the first key stored in the root is 6
-
D. there are 5 leaf nodes
Answer
最终有五个叶子节点,分别为 01、23、45、67、89,故 A 错误。
2-4 After deleting 9 from the 2-3 tree given in the figure, which one of the following statements is FALSE?
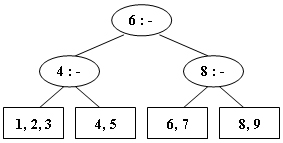
-
A. the root is full
-
B. the second key stored in the root is 6
-
C. 6 and 8 are in the same node
-
D. 6 and 5 are in the same node
Anwser
最终有 3 个叶子节点,分别为 123、45、678,故 D 错误。
2-5 Which of the following statements concerning a B+ tree of order \(M\) is TRUE?
-
A. the root always has between 2 and \(M\) children
-
B. not all leaves are at the same depth
-
C. leaves and nonleaf nodes have some key values in common
-
D. all nonleaf nodes have between \(\lceil M/2\rceil\) and \(M\) children
Answer
C. A 需要考虑根节点为叶子节点的情况,D 需要考虑根节点
Homework 4¶
1.1 The result of inserting keys 1 to \(2^k -1\) for any \(k> 4\) in order into an initially empty skew heap is always a full binary tree.
Anwser
T. 设当 \(n = k\) 时成立,那么此时最底下一层有 \(2^{k-1}\) 个叶子节点,我们先逐个插入 \(2^{k-1}\) 个节点,因为每次插入会让一个叶子节点与其兄弟节点交换并挪到左边,因此插入 \(2^{k-1}\) 个节点后之前的叶子节点会倒序且全都有一个左儿子,此时再插入 \(2^{k-1}\) 个节点会重复该流程,使得之前的叶子节点顺序又变回来且全都有左右儿子,从而使得 \(n = k + 1\) 时也成立
1.2 The right path of a skew heap can be arbitrarily long.
Anwser
T. 或许是考虑到左倾树的右路径长度是 \(O(\log N)\),而斜堆是 \(O(N)\)
2.2 We can perform BuildHeap for leftist heaps by considering each element as a one-node leftist heap, placing all these heaps on a queue, and performing the following step: Until only one heap is on the queue, dequeue two heaps, merge them, and enqueue the result. Which one of the following statements is FALSE?
-
A. in the \(k\)-th run, \(\lceil N/2^k \rceil\) leftist heaps are formed, each contains \(2^k\) nodes
-
B. the worst case is when \(N=2^K\) for some integer \(K\)
-
C. the time complexity \(T(N) = O(\frac{N}{2}log 2^0 + \frac{N}{2^2}log 2^1 + \frac{N}{2^3}log 2^2 + \cdots + \frac{N}{2^K}log 2^{K-1})\) for some integer \(K\) so that \(N=2^K\)
-
D. the worst case time complexity of this algorithm is \(\Theta (NlogN)\)
Anwser
D. 虽然 D 显然是错误的,但是 A 看着似乎也是错的
Homework 7¶
Which one of the following is the lowest upper bound of \(T(n)\) for the following recursion \(T(n) = 2T(\sqrt{n}) + \log n\)?
-
A. \(O(\log n\log \log n)\)
-
B. \(O(\log^2 n)\)
-
C. \(O(n\log n)\)
-
D. \(O(n^2)\)
Anwser
A. 显然答案应该是 \(\log n\) 乘上深度 \(k\),对深度 \(k\) 我们有 \(2^{2^k} = n\),所以 \(k = O(\log \log n)\)
Homework 8¶
2-2 In dynamic programming, we derive a recurrence relation for the solution to one subproblem in terms of solutions to other subproblems. To turn this relation into a bottom up dynamic programming algorithm, we need an order to fill in the solution cells in a table, such that all needed subproblems are solved before solving a subproblem. Among the following relations, which one is impossible to be computed?
-
A. \(A(i, j) = min (A(i-1,j), A(i,j-1), A(i-1,j-1))\)
-
B. \(A(i, j) = F(A(min\{i, j\} - 1, min\{i, j\} - 1), A(max\{i, j\} - 1, max\{i, j\} -1))\)
-
C. \(A(i, j) = F(A(i, j -1), A(i - 1, j - 1), A(i - 1, j + 1))\)
-
D. \(A(i,j) = F(A(i-2, j-2), A(i+2,j+2))\)
Anwser
D. 显然 D 无法按照顺序填表